ریاضیات شانه ای بر زلف پریشان هستی
ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباستریاضیات شانه ای بر زلف پریشان هستی
ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباست14 روش برای حل یک مسئله
| ||
| ||
مشتق
مشتق یکی از دو مفهوم اصلی حسابان است که نرخ لحظه‌ای (یا نقطه‌ای) تغییرات تابع را نشان می‌دهد.
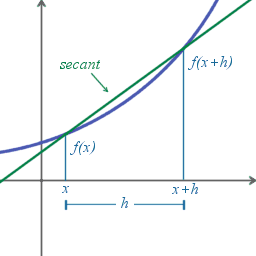
تعریف
مشتقّ تابعی مانند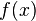 
، تابع دیگری مثل 
است که مقدارش در x با معادلهٔ زیر تعریف می‌شود:
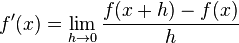
به شرطی که این حد موجود و متناهی باشد.
بر طبق این تعریف، مقدار مشتق برابر نرخ تغییرات مقدار تابع است زمانی که تغییرات مربوط به متغیر مستقل به سمت صفر میل می‌کند.
نحوهٔ نمایش.......
ادامه مطلب ...
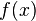، تابع دیگری مثل است که مقدارش در x با معادلهٔ زیر تعریف می‌شود: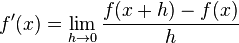نردبان موبیوس
در حوزهٔ نظریه گراف، نردبان موبیوس Mnیک گراف دورانی مکعبی با تعداد رئوس زوج nاست، که از یک n-دور و چند یال به نام پله(rungs)که جفت رئوس مخالف دور را به هم وصل می‌کنند، تشکیل شده است.این گراف به این دلیل که دقیقا n/2تا 4-دور(McSorley 1998)دارد که به وسیله یال‌های مشترکشان به هم متصل اند و یک نوار موبیوس توپولوژیکی تشکیل می‌دهند، این گونه نام گذاری شده است.نردبان موبیوس اولین بار به وسیلهٔ Guy وHarary مورد مطالعه قرار گرفت و نام گذاری شد.اگر علاقمند هستید ادامه مطلب را بخوانید........
درخت اسپلی
درخت اسپلی (به انگلیسی: Splay tree) یک درخت جستجوی دودویی خود متعادل است. که از قابلیت‌های جدیدی برخوردار می‌باشد که دسترسی به اطلاعات جدیدا دسترسی یافته را سهولت می‌بخشد. و عناصری که اخیرا دسترسی یافته اند سریعتر مورد دسترسی قرار می گیرند.این درخت اعمال اساسی مانند درج و جستجو و حذف را در(o(lgnانجام می دهد. برای خیلی از دنباله‌های غیر یکنواخت، بهتر از سایر درخت‌های جستجو عمل می کند.درخت اسپلی به وسیله «دانیل اسلیتور» و «رابرت تارجان» در سال 1985 اختراع شد. همهٔ عملیات معمول در درخت جستجوی دودویی با یک عمل پایه به نام splaying ترکیب می شوند.به این معنی که برای یک عنصر خاص درخت را باز می آراید تا عنصر در ریشهٔ درخت قرار بگیرد.یک راه انجام این کار این است که ابتدا یک جستجو برای یافتن عنصر مورد نظر انجام می دهیم وسپس آن را به بالای درخت می رسانیم. 
........
درخت (ساختار داده)
محتویات |
در علوم کامپیوتر، درخت ساختار دادهٔ پر استفاده است که شبیه به یک ساختار درختی با مجموعه‌ای از گره‌های متصل به هم است. درخت یک گراف همبند بدون دور است. اکثر نویسندگان این قید را نیز اضافه می‌کنند که گراف باید بدون جهت باشد. یه علاوه بعضی قید بدون وزن بودن یالها را نیز اضافه می‌کنند.
محاسبه ذهنی
محاسبه ذهنی شامل محاسبات ریاضی تنها با استفاده از توانایی‌های مغز انسان بدون کمک ماشین حساب، کامپیوتر، خودکار و یا کاغذ است. برای نمونه می‌توان از روش‌های محاسبه یاکوف تراختنبرگ نام برد.
روش‌های محاسبه ذهنی عمل ضرب
در این روش عمل محاسبه بدون استفاده از جدول ضرب و صرفا به وسیله عمل جمع انجام می‌گیرد. به کمک این روش به صورت ذهنی می‌توان به راحتی اعداد بسیار بزرگ را در هم ضرب و جواب صحیح را بدست آورد.
روش ضرب اعداد در عدد ۱۱
- روش تراختنبرگ برای ضرب اعداد مختلف در عدد یازده به صورت زیر است:
- ۱- آخرین عدد مضروب (عددی که در یازده ضرب می‌شود) را به عنوان رقم سمت راست جواب می‌نویسیم
- ۲- هر عدد متوالی از مضروب با همسایه طرف راست آن جمع می‌شود
- ۳- اولین عدد مضروب، رقم سمت چپ جواب می‌شود. این آخرین مرحله محاسبه‌است
- مثال: ۱۱×۶۳۳
- حل:
- ۱- آخرین رقم ۶۳۳ اولین رقم سمت راست جواب است. یعنی عدد۳
- ۲- هر رقم متوالی از عدد۶۳۳ با همسایه طرف راست آن جمع می‌شود، یعنی ۳+۳ می‌شود که از آن عدد ۶ به دست می‌آید. این دستور را دوباره به همان شکل تکرار می‌کنیم، اینبار ۳+۶ که از آن عدد ۹ به دست می‌آید.
- ۳- اولین رقم ۶۳۳ یعنی ۶، اولین رقم سمت چپ جواب می‌شود.
- بنابر این حاصلضرب ۶۳۳×۱۱ می‌شود ۶۹۶۳
روش ضرب اعداد در عدد ۱۲.......
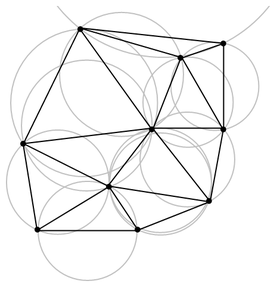
مثلث بندی دیلانی
در ریاضیات و هندسه‌ی محاسباتی، یک مثلث‌بندی دیلانی برای یک مجموعه از نقاط به نام P در یک صفحه، یک مثلث‌بندی به نام (DT(P است به نحوی که هیچ یک از نقاط P در هیچ‌یک از دایره‌های محیطی مثلثهای (DT(P نباشد. این مثلث‌بندی کمینه‌ی زاویه‌های مثلثها را به بیشترین مقدار ممکن می‌رساند و به این ترتیب از به وجود آمدن مثلثهای باریک جلوگیری می‌کند. این مثلث‌بندی توسط بوریس دیلانی در سال ۱۹۳۴ ابداع شد(منبع:سایت ویکی پدیا)
![\sum_{m=1}^n m^3 = \left[\frac{n(n+1)}{2}\right]^2 = \frac{n^4}{4} + \frac{n^3}{2} + \frac{n^2}{4} = \left(\sum_{m=1}^n m\right)^2\,\!](http://upload.wikimedia.org/math/3/b/8/3b866c924645dbbb11831b06b18e2b61.png)
-اُم، و 
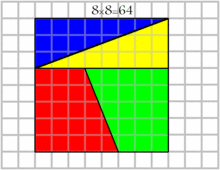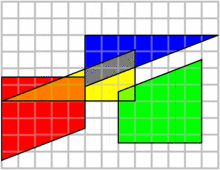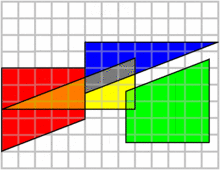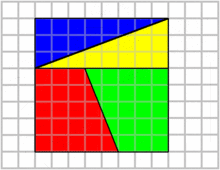
عددی منفی است.تجزیه سم لوید :
چهار قطعه با مجموع مساحت ۶۴ در کنار هم قرار گرفته‌اند ولی بعد از جابه‌جایی ۱ واحد به مساحت آنها اضافه می‌شود در حالی که قطعات تغییری نکرده‌اند پس مساحت کل هم نباید تغییر می‌کرد!
علت این پدیده، شیب متفاوت قطعه‌ها است، برای مثال قطعه آبی و سبز در حالت دوم هم‌پوشانی دارند و قسمتی از هر کدام با هم منطبق می‌شوند. شیب وتر قطعه آبی برابر ۰٫۳۷۵ است که روی ضلعی از قطعه سبز قرار می‌گیرد که شیب آن ۰٫۴ است. نزدیکی شیب‌ها باعث می‌شود این تفاوت در نگاه اول نمایان نشود.
منبع :سایت ویکی پدیا
معما
معمای مربع گم‌شده معمایی متأثر از خطای دید است که در کلاس‌های درس ریاضیات به منظور به کارگیری تجسم هندسی دانش‌آموزان مطرح می‌شود.
این پازل دو ترکیب از اشکالی را نشان می‌دهد که ظاهراً در مجموع، دو مثلث قائم‌الزاویهٔ هم‌نهشت هستند. اما یکی از آنها یک مربع ۱×۱ فضای خالی دارد.
محاسبه ی مساحت دایره
خوب، فقط نگاه کنید ... آسان است.
با دایره ای که می خواهیم بشکنیم شروع می کنیم.
حالا دایره را به چهار قسمت مساوی تقسیم می کنیم.
 | | | |
سؤالات و کلید اولیه گروه‌های آزمایشی علوم ریاضی و فنی،علوم تجرب
آزمون سراسری سال ۱۳۸۹
گروه آزمایشی | دفترچه عمومی | دفترچه اختصاصی | کلید اولیه آزمون |
علوم ریاضی و فنی |
|
|
|
هنر |
|
|
|
علوم تجربی |
|
|
|
زبان‌های خارجی |
|
|
|
علوم انسانی |
|
|
|
طرح و تنظیم از : | # |
منبع:سایت سازمان سنجش آموزش کشور
باتشکر از گروه ریاضی استان اذربایجان غربی
ریاضیات و شناخت
آرتور هاید 2 ترجمه ی دبیر ریاضی راهنمایی و دانشجوی دکتری ریاضی با گرایش آموزش ریاضی مقدمه در کشورهایی که امتیاز بالایی در مسابقات بین المللیِ موفقیت ریاضی کسب کرده اند، کلاس های درس ریاضی یک وجه اشتراک دارند [و آن] فرهنگِ تدریس و یادگیری است که به دانش آموزان کمک می کند ارتباطات و اتصالات را برقرار سازند و درک مفهومی را بنا نهند. این اظهارنظر از درس های ویدیویی معلمان پایه ی هشتم نتیجه شده است. این درس های ویدیویی از علوم کشورها، معلمان، نه تنها به دان شآموزان مسائل ریاضی چال شبرانگیز محول می کنند، بلکه از پرسش و گفتگوی تا به دانش آموزان کمک کنند که حین حل این مسئله ها، ارتباطات و اتصالات بین مفاهیم بین مفاهیم ریاضی را دیده و درک نمایند.
تاریخچه عدد صفر
یکی از معمول ترین سئوالهائی که مطرح می شود این است که: چه کسی صفر را کشف کرد؟ البته برای جواب دادن به این سئوال بدنبال این نیستیم که بگوئیم شخص خاصی صفر را ابداع و دیگران از آن زمان به بعد از آن استفاده می کردند.
اولین نکته شایان ذکر در مورد عدد صفر این است که این عدد دو کاربرد دارد که هر دو بسیار مهم تلقی می شود یکی از کاربردهای عدد صفر این است که به عنوان نشانه ای برای جای خالی در دستگاه اعداد (جدول ارزش مکانی اعداد) بکار می رود. بنابراین در عددی مانند 2106 عدد صفر استفاده شده تا جایگاه اعداد در جدول مشخص شود که بطور قطع این عدد با عدد 216 کاملاً متفاوت است. دومین کاربرد صفر این است که خودش به عنوان عدد بکار می رود که ما به شکل عدد صفر از آن استفاده می کنیم.
تضعیف مکعب
تضعیف مکعب، یکی از سه مسئله هندسی مشهور در یونان باستان و مسئله‌ای مهم در ریاضیات دوره اسلامی است. (دو مسئله دیگر: تثلیث زاویه ، تربیع دایره).
موضوع این مسئله، ساختن مکعبی با حجم دو برابر مکعب مفروض دیگر است که نخستین بار پیش از سال ۴۵۰ ق.م مطرح شد. بر اساس افسانه‌هایی این مسئله منشأ دینی دارد: ساختن محرابی با حجم دو برابر محراب مفروضِ دیگر چنانکه شکل هر دو محراب یکسان (مثلاً هر دو مکعب) باشد.
تعبیر جبری این مسئله آن است که ریشه سوم (کعب) عدد ۲ را به دست آوریم. بقراط (ح ۴۵۰ ق.م ) این مسئله را به صورت درج دو واسطه تناسب میان دو مقدار (یا دو پاره خط ) معلوم a و b مطرح کرد.
در قرن چهارم پیش از میلاد و پس از آن، بسیاری از هندسه‌دانان یونانی، حالت‌های گوناگون واسطه‌های تناسب میان دو خط معلوم را بررسی کردند.
در اینجا فهرستی از هندسه‌دانان و روش‌های آنان برای حل این مسئله آمده‌است: .....
ادامه مطلب ...تست ریاضی پایه
استدلالها
1. با شنیدن صدای آژیر آمبولانس نتیجه گیری می کنیم که بیماری را به بیمارستان منتقل می کنند. از کدام استدلال استفاده کرده ایم؟
الف. استقرای ریاضی ب. استدلال استنتاجی ج. استدلال تمثیلی د. درک شهودی
2. پاستور دانشمند علوم تجربی بسیاری از بیماری ها را با استفاده از داروهای که کشف نمود معالجه کرد، روش کار او بر مبنای کدام استدلال بوده است؟
الف. درک شهودی ب. استدلال تمیثلی ج. استدلال استقرایی د. استدلال استنتاجی
3. از حرارت دادن میله های فلزی مختلف درآزمایشگاه نتیجه گرفته شده است که میلههای فلزی در اثر حرارت طولشان زیادیم شود نوع استدلال برای این نتیجه گیری کدام است؟
الف. استدلال استنتاجی ب. استدلال تمثیلی ج. استدلال استقرایی د. استدلال قیاسی
4. افراد قبیله ای اوقات شرعی خود را با سایه ی اشیاء ؟؟؟ ستارگان تشخیص یم دهند این افراد کدام استدلال را به کار می برند.......
ادامه مطلب ...قدرت اعداد
سال ها پیش در یکی از کلاس های ریاضیات مدارس آلمان، آموزگار برای اینکه مدتی بچه ها را سرگرم کند و به کارش برسد؛ از آنها خواست تا مجموع اعداد از یک تا صد را حساب کنند. پس از چند دقیقه یکی از شاگردان کلاس گفت: مجموع این اعداد را پیدا کرده و حاصل عدد ۵۰۵۰ می شود. با شنیدن این عدد معلم با حیرت فراوان او را به پای تخته برد تا روش محاسبه خود را توضیح دهد. به نظر شما این شاگرد باهوش که بعدها یکی از بزرگ ترین و معروف ترین ریاضیدانان دنیا شد، چه روشی را به کار بست؟ او اعداد یک تا صد را به ردیف پشت سرهم نوشت، سپس بار دیگر همین اعداد را بالعکس، این بار از صدتا یک، درست در ردیف زیرین اعداد قبلی نوشت. طوری که هر عدد زیر عدد ردیف بالاتر قرار گرفت.وی مشاهده کرد که مجموع هر کدام از ستون های به وجود آمده ۱۰۱ است. سپس نتیجه گرفت که صد تا عدد ۱۰۱ داریم که حاصل مجموع آنها می شود ۱۰۱۰۰=۱۰۱*۱۰۰. پس از آن تنها کافی بود که این مجموع به دست آمده نصف شود یعنی:
۵۰۵۰=۲/۱۰۱۰۰
شاید «شارل فردریک گاوس» شاگرد با ذکاوت کلاس که این روش جالب را به کاربرد، آن هنگام نمی دانست، روش بسیار کارا و مفیدی را برای جمع بستن رشته ای از اعداد ارائه داده است که تا سالیان سال مورد استفاده ریاضیدانان خواهد بود.اکثر مفاهیم ریاضی به قدری با زندگی روزمره ما گره خورده است که تمام مردم بدون آگاهی داشتن و واقف بودن به آن، از کنارش می گذرند و تنها کاربر خوبی هستند و بس! حتماً تا