ریاضیات شانه ای بر زلف پریشان هستی

ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباست

ریاضیات شانه ای بر زلف پریشان هستی

ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباست

درخت اسپلی

درخت اسپلی (به انگلیسی: Splay tree) یک درخت جستجوی دودویی خود متعادل است. که از قابلیت‌های جدیدی برخوردار می‌باشد که دسترسی به اطلاعات جدیدا دسترسی یافته را سهولت می‌بخشد. و عناصری که اخیرا دسترسی یافته اند سریعتر مورد دسترسی قرار می گیرند.این درخت اعمال اساسی مانند درج و جستجو و حذف را در(o(lgnانجام می دهد. برای خیلی از دنباله‌های غیر یکنواخت، بهتر از سایر درخت‌های جستجو عمل می کند.درخت اسپلی به وسیله «دانیل اسلیتور» و «رابرت تارجان» در سال 1985 اختراع شد. همهٔ عملیات معمول در درخت جستجوی دودویی با یک عمل پایه به نام splaying ترکیب می شوند.به این معنی که برای یک عنصر خاص درخت را باز می آراید تا عنصر در ریشهٔ درخت قرار بگیرد.یک راه انجام این کار این است که ابتدا یک جستجو برای یافتن عنصر مورد نظر انجام می دهیم وسپس آن را به بالای درخت می رسانیم.

........

محتویات

مزایا:

کارایی بهتر : کارایی بهتر برای یک درخت اسپلی به خود متوازنی آن بستگی دارد و به این که عناصری که بارها دسترسی یافته اند به ریشه نزدیکتر شوند تا سریعتر مورد دسترسی قرار بگیرند. این تقریبا برای تمام کاربردهای عملی این ساختار مزیتی است که برای پیاده سازی cache و الگوریتم garbage collection بسیار مفید است.این ساختار هنگامی کارامدتر خواهد بود که دسترسی به صورت یک پارچه نباشد.
پیاده سازی ساده تر: پیاده سازی ساده تری نسبت به دیگر درختهای جستجوی دودویی خود متوازن، مانند درخت قرمز سیاه و یا درخت هایAVL دارد.
امکان ایجاد یک نسخه پایدار: که اجازه دسترسی به هر دو نسخه قبلی و جدید را پس از بروز رسانی می دهد . این می تواند در برنامه نویسی تابعی مفید باشد و به(O(lgn فضا در هر بروز رسانی نیاز دارد.
بر خلاف سایر انواع درختان خود متعادل به خوبی با گره حاوی کلیدهای هویت کار می کند. حتی با وجود کلیدهای هویت، عملکرد در (O(lgn باقی می ماند. یک طراحی دقیق عملیات find می تواند چپ‌ترین و یا راست‌ترین گرهٔ کلید داده شده را برگرداند.

معایب

درختانی می توانند وجود داشته باشند که توزیع داده شده از ورودی را "کمی" سریعتر انجام می دهند.
عملکرد ضعیف در دسترسی یکنواخت : عملکرد درخت اسپلی بطور قابل توجهی بدتر از درخت جستجوی دودویی متعادل ساده برای دسترسی یکنواخت است.
یکی از بدترین حالت‌های الگوریتم درخت اسپلی دسترسی ترتیبی به همه عناصر در درخت مرتب شده است که درخت را کاملا نامتعادل می‌کند (این n دسترسی دارد که هرکدام از (o(lgn است). دوباره مورد دسترسی قرار دادن عنصر اول، باعث می‌شود که عملیاتی که از (O(n است اجرا شود تا درخت دوباره متوازن شود (قبل بازگشت عنصر اول).این تاخیر قابل توجهی برای عملیات نهایی است، با این حال، تحقیقات اخیر نشان می دهد که «متعادل‌سازی تصادفی» می تواند از اثر عدم تعادل جلوگیری کند و بازدهی مشابه سایر الگوریتم‌های خود متوازن بدهد .

فعالیت با Splay

هنگامی که یک گره x مورد دسترسی قرار میگیرد، ساختار درختی splay روی آن انجام می‌شود تا آن را در ریشه قرار دهد. برای این مقصود یک توالی از Splay Steps به‌انجام می‌رسد که هر مرحله این حرکت را بیش‌تر پیش می‌برد. و x را به ریشه نزدیکتر می کند. با انجام عملیات splay در گره مورد نظر بعد از هر دسترسی، گره ای که اخیرا مورد دسترسی قرار گرفته در نزدیکی ریشه درخت نگه داشته می‌شود و تقریبا متعادل باقی می ماند .

هر مرحله به سه عامل بستگی دارد :

آیا x فرزند چپ یا راست گره پدر خود p است ،
آیا گره p ریشه است یا نه، و اگر نه
آیا گره p فرزند چپ یا راست پدر خود g است ، (g پدربزرگ x می شود).

سه مرحله splayعبارتند از :

مرحله zig

این مرحله هنگامی انجام می گیرد که p ریشه باشد .درخت بر روی لبه بین x و p می چرخد.این مرحله برای مواجه با مسئله parity وجود دارد و تنها به عنوان آخرین مرحله، زمانی که x دارای عمق فرد در آغاز عملیات است، اجرا می شود.

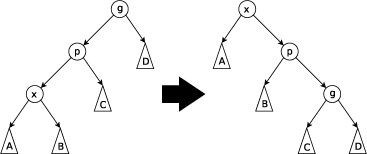
مرحله zig-zag :

این مرحله هنگامی اجرا می‌شود که p ریشه نباشد و x فرزند راست و p فرزند چپ باشد (یا بر عکس) .درخت ابتدا روی لبه بین x ,p دوران می‌کند و سپس روی لبه بین x و پدر جدیدش g دوران می کند.

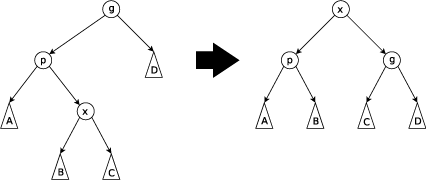
مرحله Zig-zig

این مرحله وقتی اجرا می‌شود که p ریشه نباشد و x و p هر دو فرزندان راست یا چپ باشند.تصویر زیر حالتی را نشان می دهد که x ,p هر دو فرزندان چپ هستند.درخت ابتدا روی لبه اتصال p با پدرش g، و سپس روی لبه اتصال xبا p دوران می کند. مراحل زیگ‌زیگ تنها چیزی هستند که ساختارهای درختی درهم را از Retate to Root معرفی شده از سوی آلن و مونرو متمایز می‌سازند.

درج

برای درج گره x به درخت اسپلی، ما ابتدا آن را مانند درخت دودویی جستجوی نرمال درج می کنیم .سپس با الگوریتم اسپلی گره جدید را به بالای درخت می آوریم.

حذف

برای حذف گره x، از همان روش درخت دودویی جستجو استفاده می کنیم.اگر x دو بچه داشت، ما مقدار آن را با راست‌ترین گرهٔ زیر درخت چپ آن (in-order predecessor )یا چپ‌ترین گرهٔ زیر درخت راست آن (in-order successor )جایگزین می کنیم.سپس آن گره را حذف می کنیم.در این روش پاک کردن، به حذف گره با 0 یا 1 بچه کاهش می یابد.پس از حذف، پدر گرهٔ حذف شده را به بالای درخت می آوریم.

برنامه درخت اسپلی به زبان C

در برنامهٔ زیر ایده ساختن درخت اسپلی، به زبان C است: X گره ای است که عملیات اسپلی روی آن اجرا می‌شود و root ریشه درخت است.

void splay (struct node *x, struct node *root

{
 node *p,*g;
 /*check if node x is the root node*/
 if(x==root);
 /*Performs Zig step*/
 else if(x->parent==root)
 {
  if(x==(x->parent)->left)
   rightrotation(root);
  else
   leftrotation(root);
 }
 else
 {
  p=x->parent; /*now points to parent of x*/
  g=p->parent; /*now points to parent of x's parent*/
  /*Performs the Zig-zig step when x is left and x's parent is left*/
  if(x==p->left&&p==g->left)
  {
   rightrotation(g);
   rightrotation(p);
  }
  /*Performs the Zig-zig step when x is right and x's parent is right*/
  else if(x==p->right&&p==g->right)
  {
   leftrotation(g);
   leftrotation(p);
  }
  /*Performs the Zig-zag step when x's is right and x's parent is left*/
  else if(x==p->right&&p==g->left)
  {
   leftrotation(p);
   rightrotation(g);
  }
  /*Performs the Zig-zag step when x's is left and x's parent is right*/
  else if(x==p->left&&p==g->right)
  {
   rightrotation(p);
   leftrotation(g);
  }
  splay(x, root);
 }
}