ریاضیات شانه ای بر زلف پریشان هستی

ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباست

ریاضیات شانه ای بر زلف پریشان هستی

ریاضیات هم علم است و هم هنر .علم بدان معنا که کشف می کند و هنر بدان معنا که زیباست

سریها

حاصل‌جمع سری‌های توانی

$\sum_{m=1}^n m = \frac{n(n+1)}{2}\,\!$

$\sum_{m=1}^n m^2 = \frac{n(n+1)(2n+1)}{6} = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \,\!$

$\sum_{m=1}^n m^3 = \left[\frac{n(n+1)}{2}\right]^2 = \frac{n^4}{4} + \frac{n^3}{2} + \frac{n^2}{4} = \left(\sum_{m=1}^n m\right)^2\,\!$

$\sum_{m=1}^{n} m^{4} = \frac{n(n+1)(2n+1)(3n^{2}+3n-1)}{30}=\frac{6 n^5+15 n^4+10 n^3-n}{30}\,\!$

$\sum_{m=0}^n m^s = \frac{(n+1)^{s+1}}{s+1} + \sum_{k=1}^s\frac{B_k}{s-k+1}{s\choose k}(n+1)^{s-k+1}\,\!$

که $B_k\,$ عدد برنولی $k\,$ -اُم، و $B_1\,$ عددی منفی است.

$\sum^{\infty}_{m=1} \frac{1}{m^2} = \frac{\pi^2}{6}\,\!$
$\sum^{\infty}_{m=1} \frac{1}{m^4} = \frac{\pi^4}{90}\,\!$
$\sum^{\infty}_{m=1} \frac{1}{m^{2n}} = (-1)^{n+1} \frac{B_{2n} (2\pi)^{2n}}{2(2n)!}$

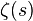$\sum_{m=1}^\infty m^{-s} = \prod_{p \text{ prime}} \frac{1}{1-p^{-s}} = \zeta(s)\,\!$

که $\zeta(s)\,$ تابع زتای ریمان است.

سری‌های توانی

برای حالت‌های نامتناهی: $| x | < 1$

$\sum_{m=0}^\infty x^m= \frac{1}{1-x}\,\!$

$\sum_{m=0}^n x^m = \frac{1-x^{n+1}}{1-x} = 1+\frac{1}{r}\left(1-\frac{1}{(1+r)^n}\right)$ که $r > 0$ و $x=\frac{1}{1+r}.\,\!$ | $\sum_{m=0}^\infty x^{2m}= \frac{1}{1-x^2}\,\!$ $\sum_{m=1}^\infty m x^m = \frac{x}{(1-x)^2}\,\!$ | $\sum_{m=1}^n m x^m = x\frac{1-x^n}{(1-x)^2} - \frac{n x^{n+1}}{1-x}\,\!$ $\sum_{m=1}^{\infty} m^2 x^m =\frac{x(1+x)}{(1-x)^3}\,\!$ $\sum_{m=1}^n m^2 x^m = \frac{x(1+x-(n+1)^2x^n+(2n^2+2n-1)x^{n+1}-n^2x^{n+2})}{(1-x)^3} \,\!$ $\sum_{m=1}^{\infty} m^3 x^m =\frac{x(1+4x+x^2)}{(1-x)^4}\,\!$ $\sum_{m=1}^{\infty} m^4 x^m =\frac{x(1+x)(1+10x+x^2)}{(1-x)^5}\,\!$ $\sum_{m=1}^{\infty} m^k x^m = \operatorname{Li}_{-k}(x),\,\!$

که $L i s (x)$ پلی‌لگاریتم x است.

سری‌های سادهٔ کسری

$\sum^{\infty}_{m=1} \frac{x^m}m = \ln\left(\frac{1}{1-x}\right)$ برای $|x| < 1 \!$

$\sum^{\infty}_{m=0} \frac{(-1)^m}{2m+1} x^{2m+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \cdots = \arctan(x)\,\!$

$\sum^{\infty}_{m=0} \frac{x^{2m+1}}{2m+1} = \mathrm{arctanh} (x)$ برای $|x| < 1\,\!$

سری‌های کسری فاکتوریلی

بسیاری از سری‌های توانی که از بسط تیلور به دست می‌آیند، ضریب‌های فاکتوریلی دارند.

$\sum^{\infty}_{m=0} \frac{x^m}{m!} = e^x$
$\sum^{\infty}_{m=0} \frac{(-1)^m}{m!} x^{m} = \frac{1}{e^{x}}$

$\sum^{\infty}_{m=0} m \frac{x^m}{m!} = x e^x$ (توزیع پواسون)
$\sum^{\infty}_{m=0} m^2 \frac{x^m}{m!} = (x + x^2) e^x$ (مشتق دوم توزیع پواسون)
$\sum^{\infty}_{m=0} m^3 \frac{x^m}{m!} = (x + 3x^2 + x^3) e^x$
$\sum^{\infty}_{m=0} m^4 \frac{x^m}{m!} = (x + 7x^2 + 6x^3 + x^4) e^x$
$\sum^{\infty}_{m=0} m^n \frac{x^m}{m!} = x \frac{d}{dx}\sum^{\infty}_{m=0} m^{n-1} \frac{x^m}{m!}$

$\sum^{\infty}_{m=0} \frac{(-1)^m}{(2m+1)!} x^{2m+1}= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots = \sin x$

$\sum^{\infty}_{m=0} \frac{(-1)^m}{(2m)!} x^{2m} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots = \cos x$

$\sum^{\infty}_{m=0} \frac{x^{2m+1}}{(2m+1)!} = \sinh x$

$\sum^{\infty}_{m=0} \frac{x^{2m}}{(2m)!} = \cosh x$

$\sum^{\infty}_{m=0} \frac{(2m)!}{4^m (m!)^2 (2m+1)} x^{2m+1} = \arcsin x\quad\mbox{ for } |x| < 1\!$

$\sum^{\infty}_{m=0} \frac{(-1)^m (2m)!}{4^m (m!)^2 (2m+1)} x^{2m+1} = \mathrm{arcsinh}(x) \quad\mbox{ for } |x| < 1\!$

$\sum^{\infty}_{m=0} \frac{(4m)!}{16^m \sqrt{2} (2m)! (2m+1)!} x^m = \sqrt{\frac{1 - \sqrt{1-x}}{x}}$ ^[۱]

$\sum^{\infty}_{m=0} \frac{4^m (m)!^2}{(m+1) (2m+1)!} x^{2m} = \left( \frac{\arcsin{x}}{x} \right)^2$ ^[۱]

$\sum^{\infty}_{m=0} \frac{\prod_{n=0}^{m-1}(4n^2+1)}{(2m)!} x^{2m} + \sum^{\infty}_{m=0} \frac{4^m \prod_{n=1}^{m}(\frac{1}{2}-n+n^2)}{(2m+1)!} x^{2m+1} = e^{\arcsin{x}}$ ^[۱]

سری‌های دوجمله‌ای

سری‌های هندسی:

$(1+x)^{-1} = \begin{cases} \displaystyle \sum_{m=0}^\infty (-x)^m & |x|<1 \\ \displaystyle \sum_{m=1}^\infty -(x)^{-m} & |x|>1 \\ \end{cases}$

بسط دوجمله‌ای:

$(a+x)^n = \begin{cases} \displaystyle \sum_{m=0}^\infty \binom{n}{m} a^{n-m} x^m & |x| \! < \! |a| \\ \displaystyle \sum_{m=0}^\infty \binom{n}{m} a^m x^{n-m} & |x| \! > \! |a| \\ \end{cases}$

$(1+x)^\alpha = \sum_{m=0}^\infty {\alpha \choose m} x^m$

برای تمام $| x | < 1$ و تمام $\alpha\!$ های مختلط

عمومی‌شدهٔ ضریب‌های دوجمله‌ای

${\alpha\choose n} = \prod_{k=1}^n \frac{\alpha-k+1}k = \frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}\!$

ریشهٔ دوم:

$\sqrt{1+x} = \sum_{m=0}^\infty \frac{(-1)^m(2m)!}{(1-2m)m!^24^m}x^m$ برای $|x|<1\!$

گوناگون:

^[۲] $\sum_{m=0}^\infty {m+n \choose m} x^m = \frac{1}{(1-x)^{n+1}}$
^[۲] $\sum_{m=0}^\infty \frac{1}{m+1}{2m \choose m} x^m = \frac{1}{2x}(1-\sqrt{1-4x})$
^[۲] $\sum_{m=0}^\infty {2m \choose m} x^m = \frac{1}{\sqrt{1-4x}}$
^[۲] $\sum_{m=0}^\infty {2m + n \choose m} x^m = \frac{1}{\sqrt{1-4x}}\left(\frac{1-\sqrt{1-4x}}{2x}\right)^n$

عددهای برنولی

$\sum_{m=0}^{\infty} \frac{B_m}{m!} x^m = \frac{x}{e^x-1}$ ^[۱]
$\sum_{m=0}^{\infty} \frac{(-4)^m B_{2m}}{(2m)!} x^{2m} = x \cot{x}$ ^[۱]
$\sum_{m=1}^{\infty} \frac{(-1)^{m-1} 2^{2m} (2^{2m}-1) B_{2m}}{(2m)!} x^{2m-1} = \tan{x}$ ^[۱]
$\sum_{m=0}^{\infty} \frac{(-1)^{m-1} (4^m-2) B_{2m}}{(2m)!} x^{2m} = \frac{x}{\sin{x}}$ ^[۱]

عددهای هارمونیک

$\sum_{m=1}^{\infty} H_m x^m = \frac{\log{\frac{1}{1-x}}}{1-x}$
$\sum_{m=2}^{\infty} \frac{H_{2m-1}}{m} x^m = \frac{1}{2} \left( \log{\frac{1}{1-x}} \right)^2$ ^[۱]
$\sum_{m=1}^{\infty} \frac{(-1)^{m-1} H_{2m}}{2m+1} x^{2m+1} = \frac{1}{2} \arctan{x} \log{(1+x^2)}$ ^[۱]
$\sum_{m=0}^{\infty} \frac{\sum_{n=0}^{2m} \frac{(-1)^n}{2n+1}}{4m+2} x^{4m+2} = \frac{1}{4} \arctan{x} \log{\frac{1+x}{1-x}}$ ^[۱]